Quicksort

Quicksort is a sorting algorithm which applies divide and conquer paradigm. Quicksort has a worst case running time of \( O(n^{2}) \) , however, it has running time of \( O(n​ logn) \) on average which makes quicksort very efficient. Moreover, it works in-place but not stable. The performance of quicksort depends on selecting the pivot, and starting to partition around it. During the partition procedure subarrays divided into four regions; \( \leq x \), \( > x \), \( unrestricted \) ,and finally the \( pivot \).

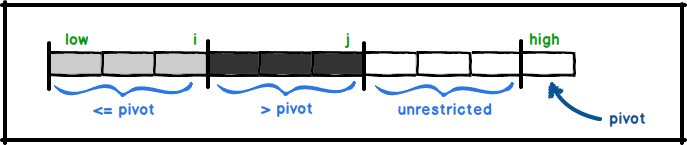
It works by selecting a pivot element and partition the array around the pivot in which left side is less than or equal to pivot ,and right side is greater than pivot. Later on two subarrays are sorted by making recursive calls to quicksort.

Algorithm

• Divide : Partition the array (A[low..high]) into two subarrays (A[low..q-1]) and (A[q+1..high]) such that each element of (A[low..q-1]) is less than or equal to (A[q]), which is less than or equal to each element of (A[q+1..high]). Compute the index q which is true place to pivot.
• Conquer : Sort the two subarrays (A[low..q-1]) and (A[q+1..high]) by recursive calls to quicksort.
• Combine : Because the subarrays are already sorted, no work is needed to combine them. Thus, the entire array (A[low..high]) is sorted.

Complexity Analysis

As it was mentioned performance of quicksort depends on the choice of pivot. So selecting always the last, first or mid element as pivot will let quicksort to run \( O(n^{2}) \) in worst case ,and space complexity will become \( O(n) \) due to the number of recursive calls. However, there are some optimizations to decrease worst case running time and space complexity which you find from wiki

Time			Space
Best case	Worst case	Average case	Worst case
\(O(nlogn)\)	\(O(n^2)\)	\(O(n​logn)\)	\(O(n) auxiliary\)

Code

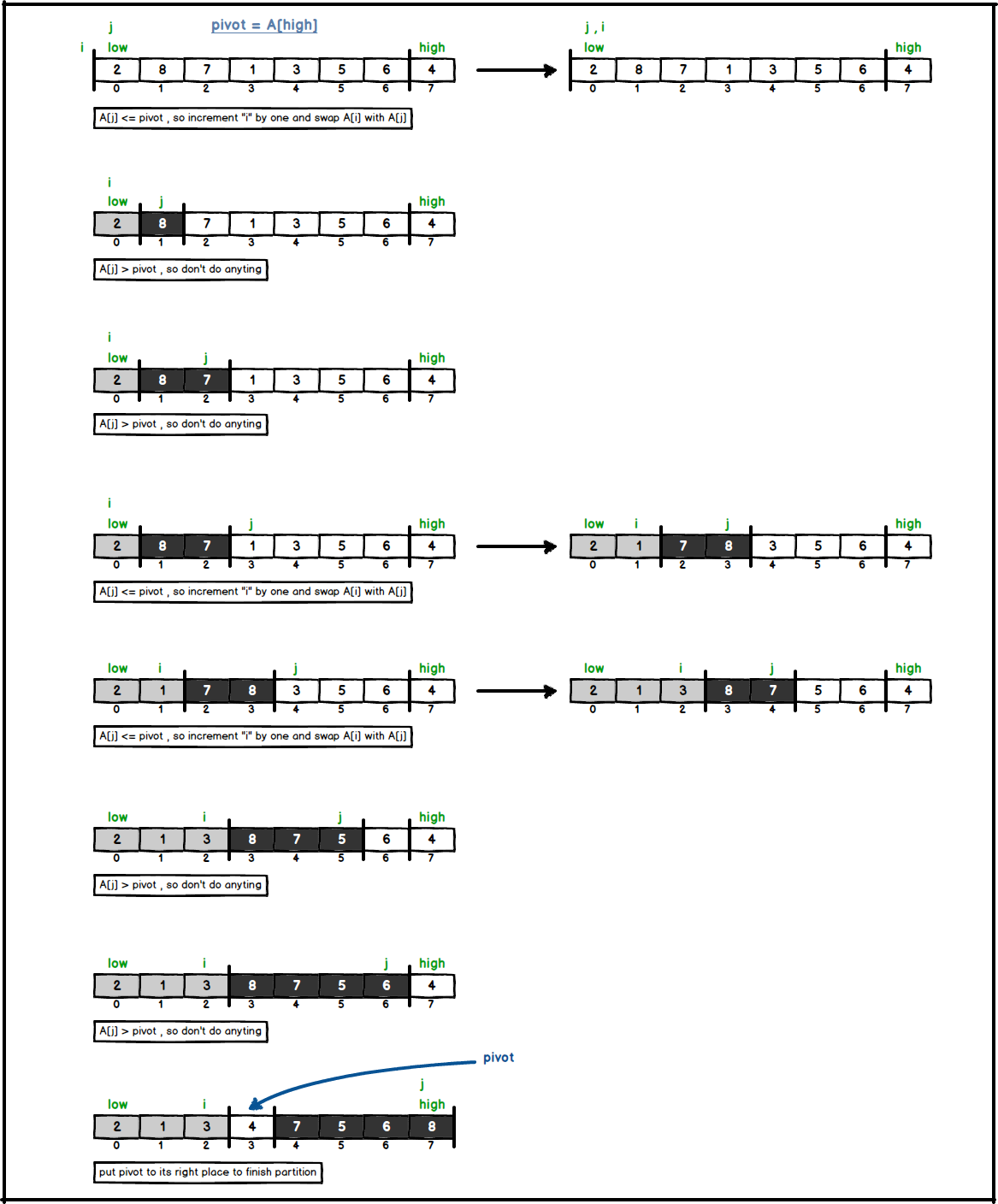
Quicksort procedure consists of a call to partition procedure which returns the index of pivot. And then, two subarrays are sorted by making recursive calls.By the way, pivot is always selected from right. A visualization of how partition procedure works on an input array is shown below ;

public void quickSort(int[] numbers, int low, int high) {
    if (low < high) {

    int q = partition(numbers, low, high);
    quickSort(numbers, low, q - 1);
    quickSort(numbers, q + 1, high);
}

private int partition(int[] numbers, int low, int high) {
    // select the right most element as pivot
    int pivot = numbers[high];

    int i = low - 1;

    for (int j = low; j < high; j++) {
      if (numbers[j] <= pivot) {
        i++;
        swap(numbers, j, i);
      }
    }

    // finally swap the pivot with the first number which is
    // greater than pivot
    swap(numbers, i + 1, high);

    // return the index of pivot
    return i + 1;
}

Randomized Pivot Selection

Pivot is selected by a randomized way to prevent from worst cases (like already sorted array as input). Instead of always selecting \( A[high] \) as the pivot, an element is randomly chosen from the subarray \( A[low..high] \). After pivot is selected it is swapped by \( A[high] \). On the other hand, by random selection every element has same probability to get selected. Thus we expect the split of the input array to be well balanced on average. Randomizedpartition procedure is shown below;

private int randomizedPartition(int[] numbers, int low, int high) {
    Random rand = new Random();
    int randomPivot = rand.nextInt(high - low + 1) + low;
    swap(numbers, randomPivot, high);
    return partition(numbers, low, high);
}

You can find the whole code from here