Binary Search

Binary search is a searching algorithm which works on a sorted (ascending or descending) array. In each turn, the given key is compared with the key at the middle of the array, if it is equal to it then its index is returned. Otherwise, if the given key is less than key at the middle then binary search continues its operation on left sub-array \( ( A[0..Mid-1] ) \), and similarly on right sub-array \( ( A[mid+1..N-1] ) \) if given key greater than it. If the given key cannot be found then an indication of not found is returned.

Finding an item takes logarithmic time in binary search. Thus, it works blazingly fast on huge input sets. For example, only 16 iteration is needed to search for an int value on a 2GB array. The step by step work flow is as follows;

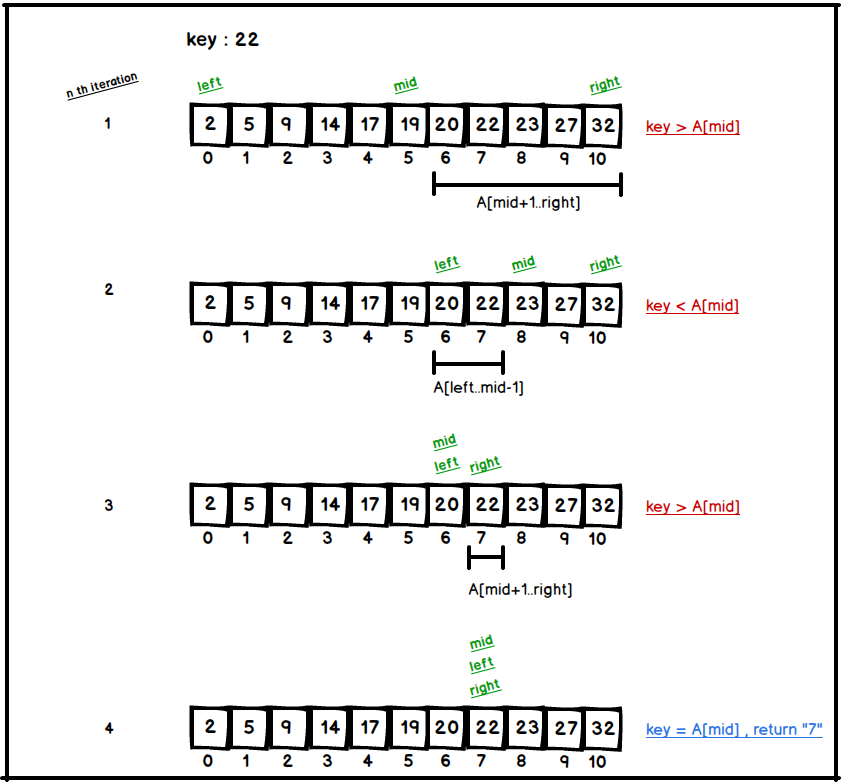
1. Check if key = A[mid] .
2. If key > A[mid] , then continue to search from right half, and return to step 1.
3. If key < A[mid] , then continue to search from left half, and return to step 1.

Complexity Analysis

Time			Space
Best Case	Average Case	Worst Case	Worst Case
\(O(1)\)	\(O(lgn)\)	\(O(lgn)\)	\(O(1) auxiliary\)

An illustration of searching a key 22 is shown below;

Code

public int binarySearch(int[] numbers, int left, int right, int key) {
    if (left <= right) { // recurse until length of array is 1
      int mid = (left + right) / 2;

      if (key == numbers[mid]) {
        return mid;
      }

      if (key > numbers[mid]) { // continue from right sub-array
        return binarySearch(numbers, mid + 1, right, key);
      } else { // continue from left sub-array
        return binarySearch(numbers, 0, mid - 1, key);
      }
    }

    return -1;
}