Graphs

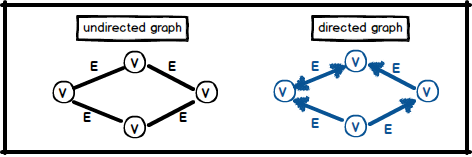
Graphs are data structures to represent road networks, the web, social networks etc. Moreover, hundreds of computational problems are related to graphs.They have two main ingredient which are;

• \(Vertices (V)\) as known as nodes.
• \(Edges (E)\) : pair of vertices
  • can be undirected.
  • or directed.

When we are talking about of a graph, \( G = (V , E) \) notation refers to a graph \( G \) which has \( |V| \) number of vertices and \( |E| \) number of edges.

Graph Representations

Graphs are commonly represented by two ways related to their structures. These are:

• Adjacency List Representation
• Adjacency Matrix Representation

Both representation has their own advantages and disadvantages. Adjacency list is preferred when the graph is sparse; which means \( |E| \) is much less than \( |V^{2}| \). Adjacency matrix is preferred when the graph is dense; which means \( |E| \) is close to \( |V^{2}| \).

1. Adjacency Matrix

Adjacency matrix of a graph \( G = (V , E) \) consists of a \( |V| ​ x ​|V| \) matrix A where;

• \(A_{ij}\) = 1 if G has an i-j edge.
• \(A_{ij}\) = 0 otherwise.

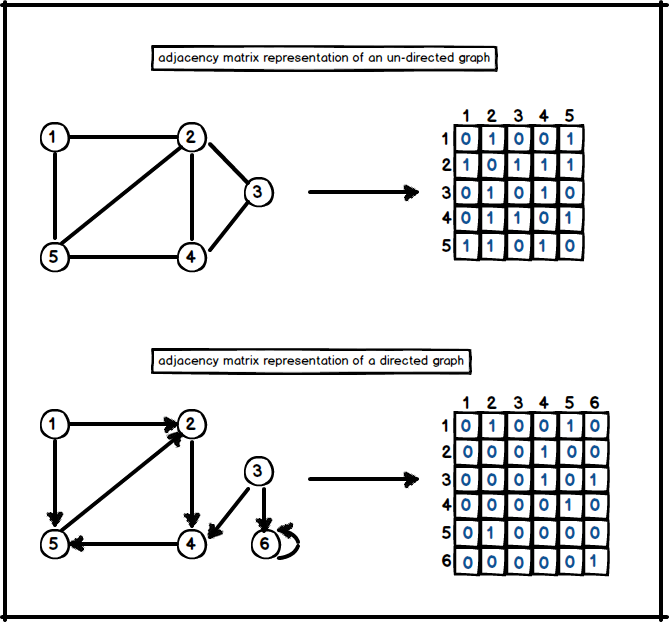
The adjacency matrix representation of a graph requires \( \theta(V^{2}) \) memory space indepently on \( |E| \).

2. Adjacency List

Adjacency list representation of a graph G = (V , E) contains an array of vertices – lets call it Adj -, and for each vertex \( u \in V \), the adjacency list \( Adj[u] \) contains all adjacent vertices \( v \) such that there is an edge \( (u , v) \in E \). In other words, \( Adj[u] \) has an array which contains only adjacent vertices to it. Thus, we can briefly say the main ingredients are;

• array (or list) of vertices.
• array (or list) of edges.

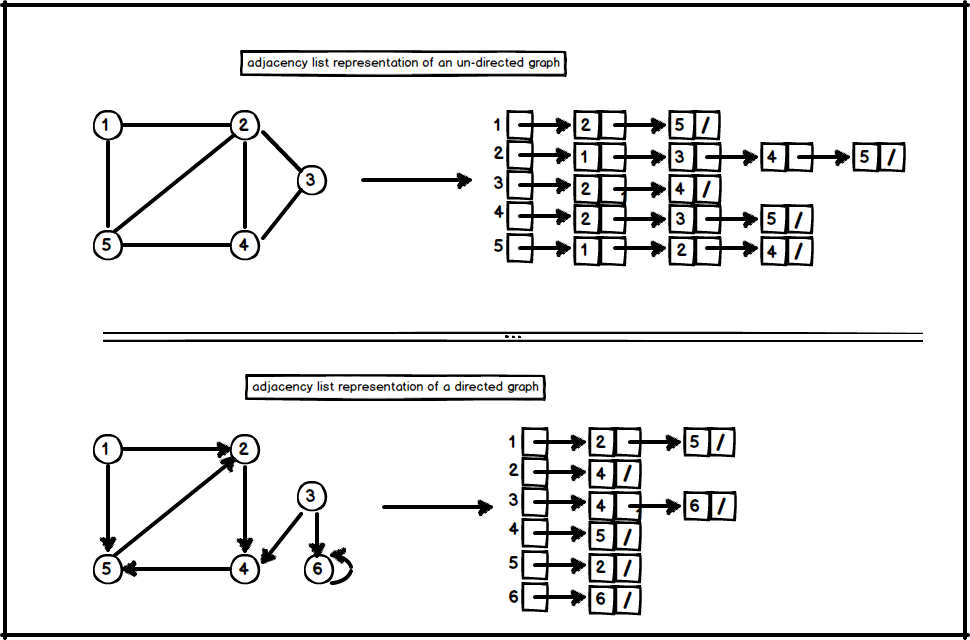
The memory for adjacency list requires \( \theta (V+E) \).

Graph Search

Now we will see two main algorithm to search a graph;

• Breadth first search.
• Depth first search.

1. Breadth First Search

Breadth first search explores graph level by level with using a queue data structure. By this search behavior we are able to compute shortest paths in a given graph \( G = (V , E) \). The algorithm starts from a given source vertex s ,and it searches it’s adjacent level of vertices ,and goes on.

• Initialize each vertex except the source.
• Take vertex v from the queue.
• Iterate each node u in adjacency list of v if it is unvisited.
• Put every node u in queue and mark it as visited.

A visual illustration is shown below;

The Vertex class looks like below;

public class Vertex {
    private boolean           visited;
    private int               distance;
    private Vertex            parent;
    private ArrayList<Vertex> adjList;
    private final String      label;

    // getters and setters
}

and the code of breadFirstSearch procedure can be seen below;

public void breadthFirstSearch(ArrayList<Vertex> graph, Vertex source) {

    // check if graph or source is null
    if (graph == null || source == null) {
      throw new IllegalArgumentException("Parameters are illegal");
    }

    initVertices(graph, source);
    initSourceVertex(source);

    Queue<Vertex> queue = new LinkedList<>();
    queue.add(source);

    while (!queue.isEmpty()) {
        // take next vertex from the queue
        Vertex v = queue.poll();

        // iterate in adjacency list of v
        for (Vertex u : v.getAdjList()) {

            if (!u.isVisited()) {
                // set u as visited
                u.setVisited(true);
                u.setDistance(v.getDistance() + 1);
                u.setParent(v);

                // put u in queue to be processed in next level
                queue.add(u);
            }
        }
    }
}

private void initVertices(ArrayList<Vertex> graph, Vertex source) {
    for (Vertex vertex : graph) {
        if (vertex != source) {
            vertex.setVisited(false);
            vertex.setDistance(Integer.MAX_VALUE);
            vertex.setParent(null);
        }
    }
}

private void initSourceVertex(Vertex source) {
    source.setVisited(true);
    source.setParent(null);
    source.setDistance(0);
}

The running time of initializing vertices will take \( O(V) \) time, and total running time of breadth-first search takes \( O(V + E) \).

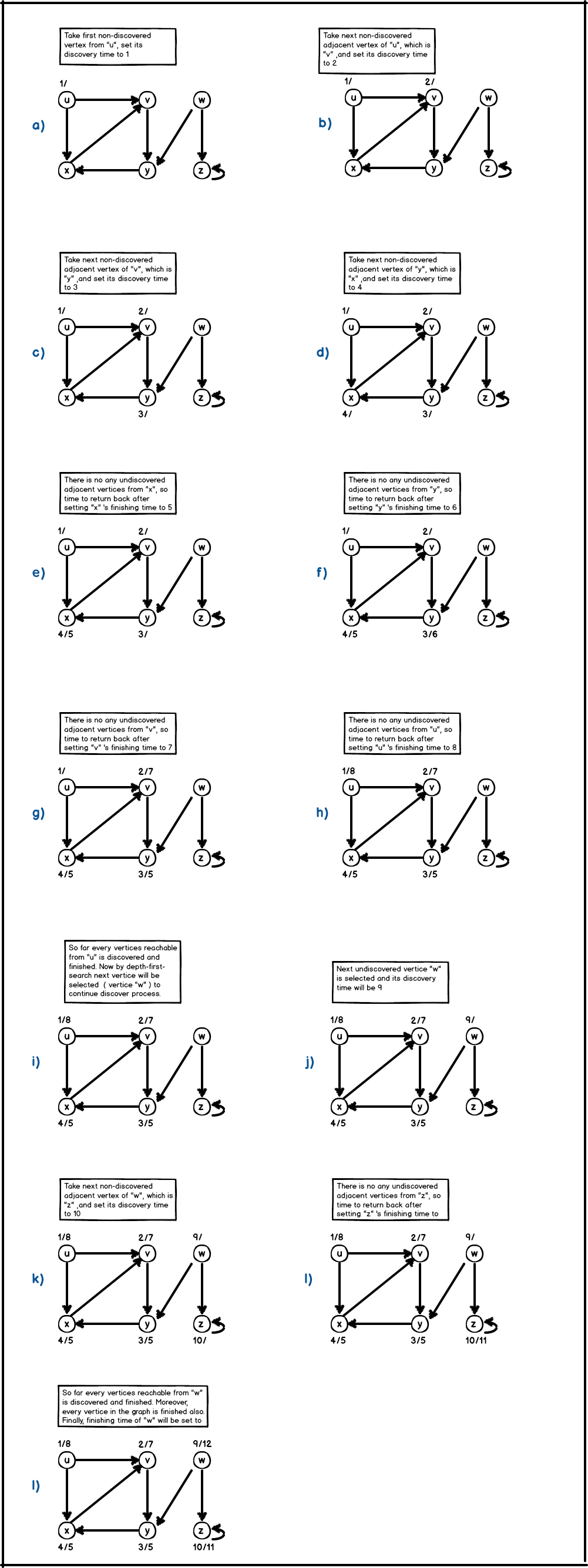
2. Depth First Search

Depth first search explores vertices by going deeper and deeper in the graph. So, at every turn an adjacent undiscovered vertex is selected from the most recently visited vertex. Whenever, a vertex is finished (when there is no any undiscovered vertex from it) then depth first search backtracks until it finds another unfinished vertex from most discovered vertex. If there is any undiscovered vertex left, then depth first search will select any undiscovered vertex as a source ,and applies dfs on it. This process continues until every vertex is finished. We are going to use discovery time and finishing time for every vertex.

• Initialize each vertex as undiscovered and set their discovery and finishing times to 0.
• Take an undiscovered vertex v from the graph and apply a depth first search on it.
• Adjust discovery time of current vertex ,and continue to search from its adjacency list. Thus, take an adjacent undiscovered vertex u from current discovered vertex, and go deeper.
• If there is no any undiscovered vertex from last discovered vertex then mark that vertex as finished, and initialize its finishing time. Later on, backtrack while until you hit an undiscovered vertex.
• Do depth first search until every vertices is finished.

A visual illustration of depth-first-search is shown below;

Vertex for depth-first-search will look like below;

public class Vertex {
    private boolean           explored;
    private boolean           finished;
    private Vertex            parent;
    private ArrayList<Vertex> adjList;
    private final String      label;
    private int               discoveredTime;
    private int               finishedTime;

    // getters and setters
}

Later on, implementation of depth-first-search class with main two procedures dfs, and dfsVisit could be seen below;

public class DepthFirstSearch {

    // global timer to set discovery and finishing times of each vertex
    private static int time = 0;

    public void dfs(ArrayList<Vertex> graph) {
        if (graph == null) {
            throw new IllegalArgumentException("Graph is null");
        }

        // init all vertices
        initVertices(graph);

        for (Vertex v : graph) {

            // select a vertex 'v' if it is unexplored
            if (!v.isExplored()) {
                // discover every vertex which are reachable from 'v'
                dfsVisit(v);
            }
        }
    }

    private void dfsVisit(Vertex v) {
        time = time + 1;

        // set discovery time of 'v'
        v.setDiscoveryTime(time);

        // set it as explored (not finished yet)
        v.setExplored(true);

        for (Vertex u : v.getAdjList()) {
            if (!u.isExplored()) {
                dfsVisit(u);
            }
        }

        time = time + 1;

        // finally all vertices reachable from 'v' are finished, so mark it as finished
        v.setFinished(true);

        // set 'v' s finis
        v.setFinishingTime(time);
    }

    private void initVertices(ArrayList<Vertex> graph) {
        for (Vertex vertex : graph) {
            vertex.setExplored(false);
            vertex.setDiscoveryTime(0);
            vertex.setFinishedTime(0);
        }
    }
}

The running time of initializing vertices will take \( O(V) \) time, and total running time of depth-first search takes \( O(V + E) \).