A Binary Search Tree (BST) is a tree data structure that supports many dynamic operations includes ;
- Search
- Minimum
- Maximum
- Insert
- Delete
- Predecessor
- Successor
Basic operations in a binary search tree take time proportional to the height of the tree. For a complete binary tree with n nodes, such operations run in (Θ(lgn)) worst-case time. If the tree is a linear chain of n nodes than the same operations will take (Θ(n)) worst-case time.
Binary Search Tree Property
There are a few properties to define a tree as a binary search tree;
- Each node x has a left child, a right child , and a parent. If x doesn't have any child it should point NULL. Only root has no parent.
- Every node is represented by a key ( this can be any kind of comparable object - we will use Integers in this example- ).
- For each node x, x's left key is less than or equal to x, and its right key is greater than x.
Here is a representation a simple BST.
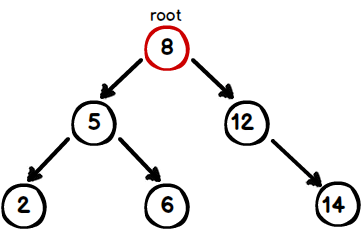
Height of BST
There are many possible trees for same set of keys. Thus, a height of a tree could be anywhere from ~log2n to ~n. Additionally, calculating height of a BST takes (O(n)) time because we have to visit every node.
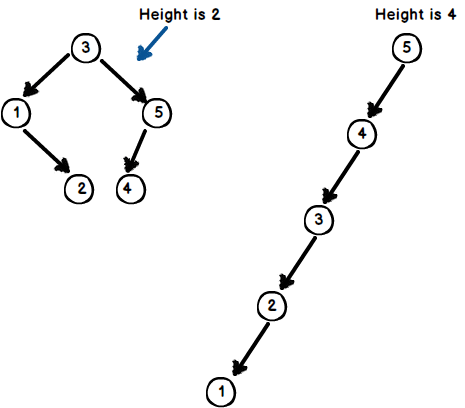
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int height(Node root) {
if (root == null) {
return 0;
}
// Height of every leaf is zero
if (root.getLeftChild() == null && root.getRightChild() == null) {
return 0;
}
int leftHeight = height(root.getLeftChild());
int rightHeight = height(root.getRightChild());
int max = Math.max(leftHeight, rightHeight) + 1;
return max;
}
Tree Walk
Inorder Tree Walk : The binary search tree property allows us to print keys in sorted order by a simple recursion algorithm which is called inorder tree walk. Walk order is;
- left subtree
- root
- right subtree
inorderTreeWalk procedure is follows;
1
2
3
4
5
6
7
public void inorderTreeWalk(Node x) {
if (x != null) {
inorderTreeWalk(x.getLeftChild());
System.out.println(x.getKey());
inorderTreeWalk(x.getRightChild());
}
}
In order tree walk take (O(n)) time because it traverses each node in the tree recursively.
Preorder Tree Walk :
Traverse order;
- root
- left subtree
- right subtree
Its running time is (O(n)) as well. Its procedure is as follows;
1
2
3
4
5
6
7
public void preorderTreeWalk(Node x) {
if (x != null) {
System.out.println(x.getKey());
preorderTreeWalk(x.getLeftChild());
preorderTreeWalk(x.getRightChild());
}
}
Postorder Tree Walk:
Traverse order;
- left subtree
- right subtree
- root
Its running time is (O(n)) as well. Its procedure is as follows;
1
2
3
4
5
6
7
public void postorderTreeWalk(Node x) {
if (x != null) {
System.out.println(x.getKey());
postorderTreeWalk(x.getLeftChild());
postorderTreeWalk(x.getRightChild());
}
}
In addition, the iterative versions of tree walks could be find at its wiki page
Query Operations
Search :
To search for a key k in BST;
- Start at the root.
-
Traverse left
(if k < current key) / right (if k > current key)child pointers as needed. - Return node with key k or NULL ,as appropriate.
1
2
3
4
5
6
7
8
9
10
11
public Node search(Node x, int key) {
while (x != null && key != x.getKey()) {
if (key < x.getKey()) {
x = x.getLeftChild();
} else {
x = x.getRightChild();
}
}
return x;
}
The running time of search procedure is (O(height)).
Minimum and Maximum :
To compute the minimum (maximum) of a BST ;
- Start at root.
- Follow left child pointers (right pointers for maximum) until you can't anymore.
- return the last key found
1
2
3
4
5
6
7
public Node treeMinimum(Node x) {
while (x.getLeftChild() != null) {
x = x.getLeftChild();
}
return x;
}
1
2
3
4
5
6
7
public Node treeMaximum(Node x) {
while (x.getRightChild() != null) {
x = x.getRightChild();
}
return x;
}
Both the procedures run in (O(height)) time.
Successor :
The successor of a node x is the node with smallest key greater than x’s key. To compute the successor of a node x ;
- Easy Case : If x's right subtree is nonempty, return minimum key in right subtree.
- Otherwise : Find the first ancestor y which is also a left child of it's parent z. Then return z.
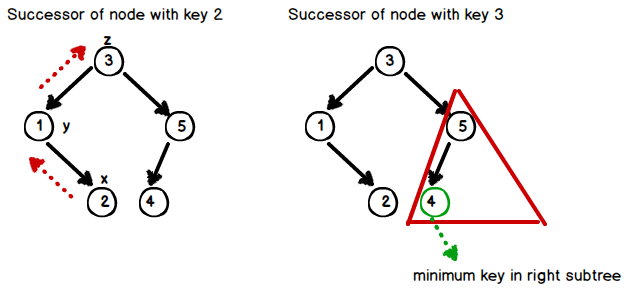
The procedure is as follow;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public Node treeSuccessor(Node x) {
if (x.getRightChild() != null) {
return treeMinimum(x.getRightChild());
}
Node parent = x.getParent();
while (parent != null && parent.getRightChild() == x) {
x = parent;
parent = x.getParent();
}
return parent;
}
Predecessor :
The predecessor of a node x is the node with greatest key less than x’s key. To compute the predecessor of a node x ;
- Easy Case : If x's left subtree is nonempty, return maximum key in left subtree.
- Otherwise : Follow parent pointers until you get to a key less than k.

The procedure is as follow;
1
2
3
4
5
6
7
8
9
10
11
12
13
public Node treePredecessor(Node x) {
if (x.getLeftChild() != null) {
return treeMaximum(x.getLeftChild());
}
Node parent = x.getParent();
while (parent != null && parent.getKey() > x.getKey()) {
parent = parent.getParent();
}
return parent;
}
Both the procedures run in (O(height)) time.
Insertion and Deletion
While insertion and deletion operations the binary search tree property should be preserved.
Insertion :
To insert a key k;
- Search a proper position for x.
- While searching maintain a trailing pointer y which is parent of x.
- Insert x as left / right child of its parent y.
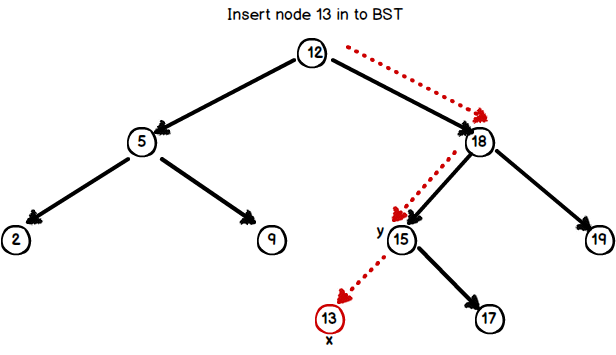
insert procedure is as follows;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public void insert(Node x) {
Node y = null;
Node z = root;
while (z != null) {
y = z;
if (x.getKey() <= z.getKey()) {
z = z.getLeftChild();
} else {
z = z.getRightChild();
}
}
// set y as x's parent
x.setParent(y);
// if root is already null then set x as root
if (root == null) {
root = x;
} else if (x.getKey() <= y.getKey()) { // set x as left child of its parent y
y.setLeftChild(x);
} else { // set x as right child of its parent y
y.setRightChild(x);
}
}
The running time of insertion is (O(height)).
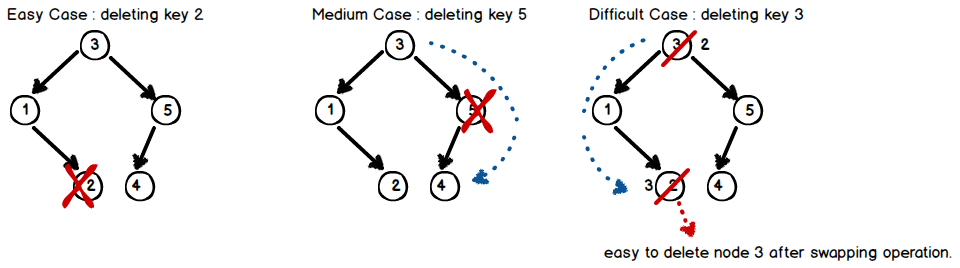
Deletion :
To delete a key k from a search tree;
- Search for k.
- Easy Case (k's no children) : Delete k's node from tree.
- Medium Case (k's one child) : Unique child has to know its parents position.
- Difficult Case (k's two children) : Compute k’s predecessor l, swap them, and deleting l will do the trick.
An illustration of deleting a key for each case;
The delete procedure will use a subroutine which is called transplant to handle with the cases when x has no children, or only one child. Transplant and delete procedures are as follows;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void delete(int key) {
Node delNode = search(root, key);
if (delNode.getLeftChild() == null) {
transplant(delNode, delNode.getRightChild());
} else if (delNode.getRightChild() == null) {
transplant(delNode, delNode.getLeftChild());
} else {
Node y = treePredecessor(delNode);
swapKeys(delNode, y);
Node z = y.getLeftChild();
transplant(y, z);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
private void transplant(Node u, Node v) {
if (u.getParent() == null) { // we delete the root
root = v;
} else if (u.getParent().getLeftChild() == u) {
u.getParent().setLeftChild(v);
} else {
u.getParent().setRightChild(v);
}
if (v != null) {
v.setParent(u.getParent());
}
}
The running time of delete procedure is (O(height)).
Here you can find the complete implementation of a BST by java.
BST
Comments powered by Disqus.