Merge Sort

Merge sort is another comparison based sort algorithm. It closely follows divide-and-conquer paradigm, and provides \( O(n​lgn) \) run time complexity in worst and average cases, however, \( O(n) \) in space complexity. Merge sort can be used for sorting huge data sets that can not fit into memory. It is also a stable sort which preserves the order of equal elements.

Algorithm

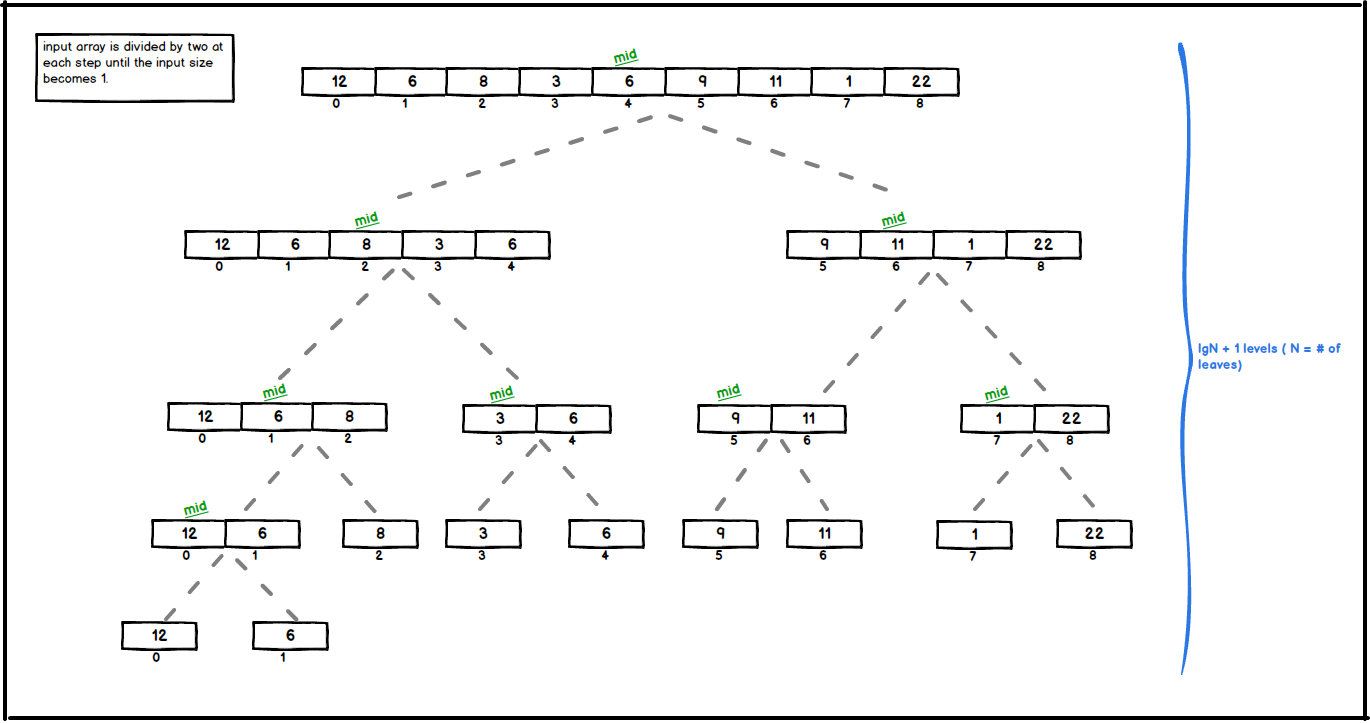
Merge sort follows a divide-and-conquer algorithm by the following steps;

• Divide : Divide the n-element sequence into two subsequences of n/2 elements each
• Conquer : Sort the two subsequences recursively using merge sort.
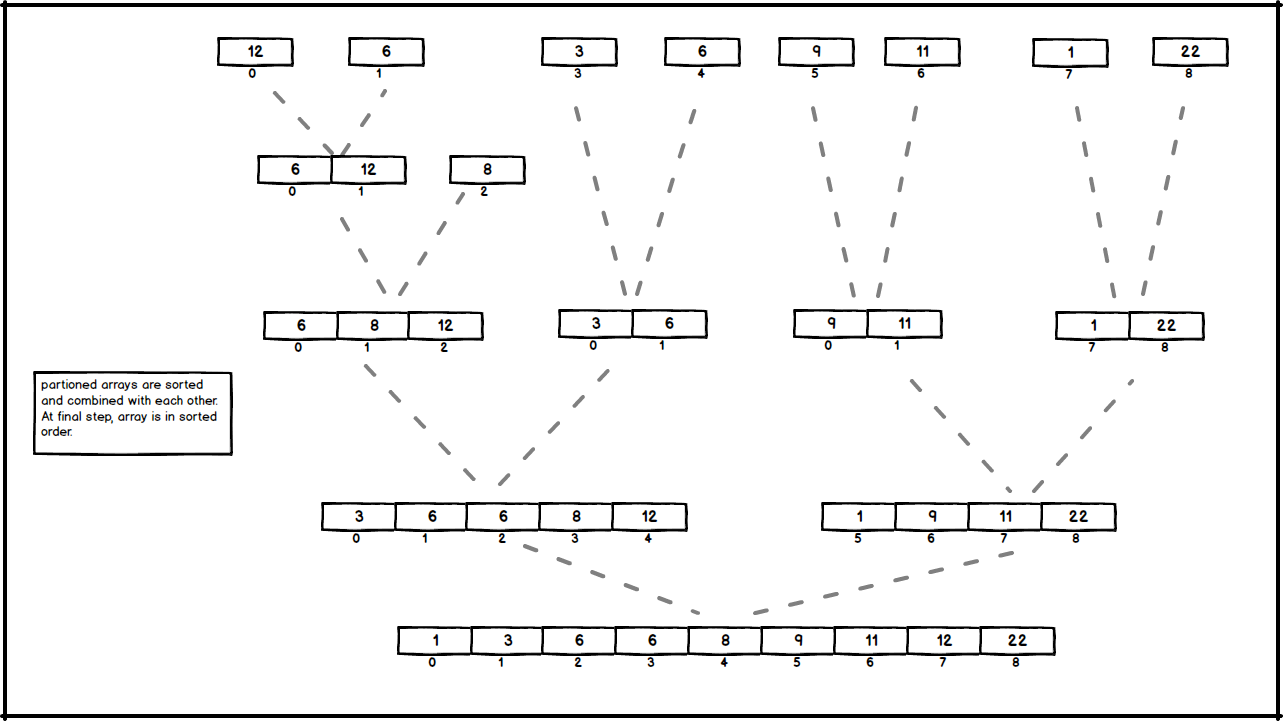
• Combine : Merge the two sorted subsequences to produce the sorted answer.

Complexity Analysis

Time			Space
Best case	Worst case	Average case	Worst case
\(O(n​lgn)\)	\(O(n​lgn)\)	\(O(n​lgn)\)	\(O(n) auxiliary\)

Code

mergeSort procedure divides input into two equal parts by recursion until input size becomes 1. Then, merge procedure sorts and combine divided parts. The code of mergeSort procedure is as following ;

public void mergeSort(int[] numbers, int left, int right) {
    if (left < right) {
      int mid = (left + right) / 2;

      // divide array into two equal parts
      mergeSort(numbers, left, mid);
      mergeSort(numbers, mid + 1, right);

      // merge part
      merge(numbers, left, mid, right);
    }
}

merge procedure is the part where subarrays are combined and sorted. Thus, merge procedure on an n-element subarray takes time \( O(n) \). Code of merge procedure is as follows;

private void merge(int[] numbers, int left, int mid, int right) {
    int[] leftArray = new int[mid - left + 1];
    int[] rightArray = new int[right - mid];

    // copy values into created arrays
    System.arraycopy(numbers, left, leftArray, 0, leftArray.length);
    System.arraycopy(numbers, mid + 1, rightArray, 0, rightArray.length);

    int leftIndex = 0;
    int rightIndex = 0;
    int k = left;

    while (leftIndex < leftArray.length && rightIndex < rightArray.length) {
      if (leftArray[leftIndex] <= rightArray[rightIndex]) {
        numbers[k] = leftArray[leftIndex];
        leftIndex++;
      } else {
        numbers[k] = rightArray[rightIndex];
        rightIndex++;
      }
      k++;
    }

    // copy rest of the left array
    while (leftIndex < leftArray.length) {
      numbers[k] = leftArray[leftIndex];
      leftIndex++;
      k++;
    }

    // copy rest of the right array
    while (rightIndex < rightArray.length) {
      numbers[k] = rightArray[rightIndex];
      rightIndex++;
      k++;
    }
}