Bubble Sort

Bubble sort is one of the simplest sorting algorithm which pairs are repeatedly compared and swapped if they are in wrong order. This process continues until no swaps are needed means that list is sorted. It takes its name from the fact that necessary elements bubble up to their correct position. Even though bubble sort shows a great performance over small input size, it has a poor performance when the input size grows. It is fast when array is in sorted order or nearly sorted. On the other hand, its worst case performance is \( O(n^{2}) \) if the array is in reversed order.

Algorithm

1. Compare each pair of adjacent elements from the beginning of the array, if a pair is in reversed order then swap the elements.
2. If there is at least one swap, then repeat first process. Otherwise, exit the loop

Let us see an example on a given array [2, 7, 9, 3, 4]

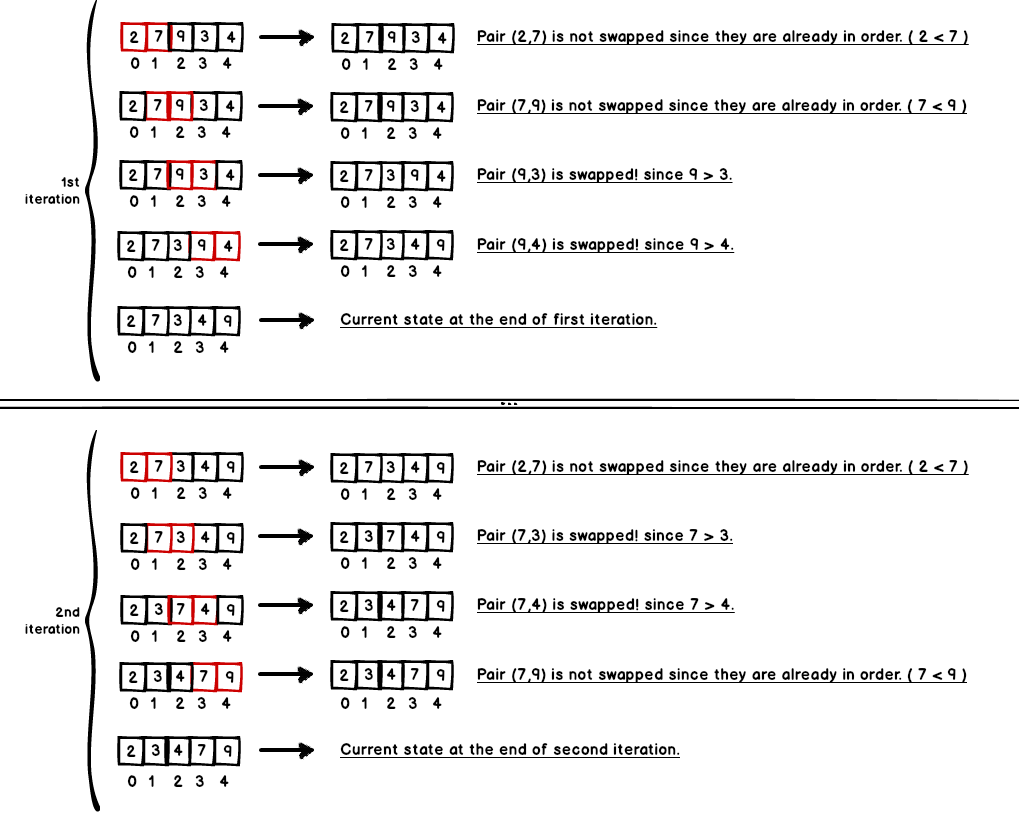
Finally, our array is sorted, however, it needs an additional iteration to figure out it is sorted. The key point is there shouldn’t be any swaps while iteration continues, so algorithm will understand that array is already sorted.

Complexity Analysis

Time			Space
Worst case	Best case	Average case	Worst case
\(O(n^{2})\)	\(O(n)\)	\(O(n^{2})\)	\(O(1) auxiliary\)

Code

public class BubbleSort {

    public void bubbleSort(int[] numbers) {
        boolean swapped = true;

        while (swapped) { // continue until there is no swap
            swapped = false;
            for (int k = 0; k < numbers.length - 1; k++) {
                if (numbers[k] > numbers[k + 1]) {
                    swap(numbers, k);
                    swapped = true; // if there is at least one swap make swapped true
                }
            }
        }
    }

    private void swap(int[] numbers, int k) {
        int temp = numbers[k + 1];
        numbers[k + 1] = numbers[k];
        numbers[k] = temp;
    }
}

And here are a bunch of test cases.

public class BubbleSortTest {

    private BubbleSort testClass;

    @Before
    public void setUp() {
        testClass = new BubbleSort();
    }

    @Test
    public void bubbleSortEx1TestSuccess() {
        int[] numbers = new int[] { 1, 7, 99, 2, 0, 12, 15 };
        testClass.bubbleSort(numbers);

        assertArrayEquals(new int[] { 0, 1, 2, 7, 12, 15, 99 }, numbers);
    }

    @Test
    public void bubbleSortEx2TestSuccess() {
        int[] numbers = new int[] { 8, 5, 3, 1, 9, 6, 0, 7, 4, 2, 5 };
        testClass.bubbleSort(numbers);

        assertArrayEquals(new int[] { 0, 1, 2, 3, 4, 5, 5, 6, 7, 8, 9 }, numbers);
    }

    @Test
    public void bubbleSortEx3TestSuccess() {
        int[] numbers = new int[] { 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 };
        testClass.bubbleSort(numbers);

        assertArrayEquals(new int[] { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }, numbers);
    }

}