Binary Search Trees

A Binary Search Tree (BST) is a tree data structure that supports many dynamic operations includes ;

• Search
• Minimum
• Maximum
• Insert
• Delete
• Predecessor
• Successor

Basic operations in a binary search tree take time proportional to the height of the tree. For a complete binary tree with n nodes, such operations run in (Θ(lgn)) worst-case time. If the tree is a linear chain of n nodes than the same operations will take (Θ(n)) worst-case time.

Binary Search Tree Property

There are a few properties to define a tree as a binary search tree;

• Each node x has a left child, a right child , and a parent. If x doesn't have any child it should point NULL. Only root has no parent.
• Every node is represented by a key ( this can be any kind of comparable object - we will use Integers in this example- ).
• For each node x, x's left key is less than or equal to x, and its right key is greater than x.

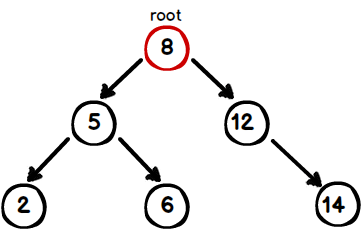
Here is a representation a simple BST.

Height of BST

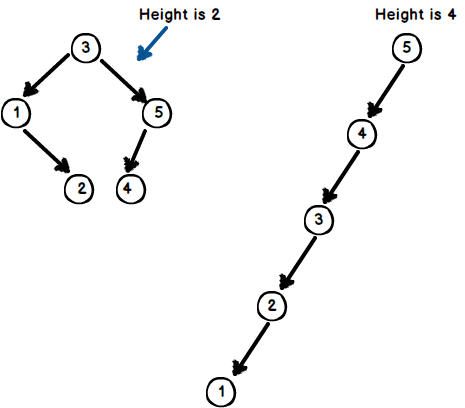
There are many possible trees for same set of keys. Thus, a height of a tree could be anywhere from ~log₂n to ~n. Additionally, calculating height of a BST takes (O(n)) time because we have to visit every node.

public int height(Node root) {
    if (root == null) {
        return 0;
    }

    // Height of every leaf is zero
    if (root.getLeftChild() == null && root.getRightChild() == null) {
        return 0;
    }

    int leftHeight = height(root.getLeftChild());
    int rightHeight = height(root.getRightChild());
    int max = Math.max(leftHeight, rightHeight) + 1;
    return max;
}

Tree Walk

Inorder Tree Walk : The binary search tree property allows us to print keys in sorted order by a simple recursion algorithm which is called inorder tree walk. Walk order is;

1. left subtree
2. root
3. right subtree

inorderTreeWalk procedure is follows;

public void inorderTreeWalk(Node x) {
     if (x != null) {

         inorderTreeWalk(x.getLeftChild());
         System.out.println(x.getKey());
         inorderTreeWalk(x.getRightChild());
     }
}

In order tree walk take (O(n)) time because it traverses each node in the tree recursively.

Preorder Tree Walk :
Traverse order;

1. root
2. left subtree
3. right subtree

Its running time is (O(n)) as well. Its procedure is as follows;

public void preorderTreeWalk(Node x) {
    if (x != null) {

		System.out.println(x.getKey());
        preorderTreeWalk(x.getLeftChild());
        preorderTreeWalk(x.getRightChild());
    }
}

Postorder Tree Walk:
Traverse order;

1. left subtree
2. right subtree
3. root

Its running time is (O(n)) as well. Its procedure is as follows;

public void postorderTreeWalk(Node x) {
    if (x != null) {

		System.out.println(x.getKey());
        postorderTreeWalk(x.getLeftChild());
        postorderTreeWalk(x.getRightChild());
    }
}

In addition, the iterative versions of tree walks could be find at its wiki page

Query Operations

Search :
To search for a key k in BST;

• Start at the root.
• Traverse left (if k < current key) / right (if k > current key) child pointers as needed.
• Return node with key k or NULL ,as appropriate.

public Node search(Node x, int key) {
    while (x != null && key != x.getKey()) {

        if (key < x.getKey()) {
            x = x.getLeftChild();
        } else {
            x = x.getRightChild();
        }
    }

    return x;
}

The running time of search procedure is (O(height)).

Minimum and Maximum :
To compute the minimum (maximum) of a BST ;

• Start at root.
• Follow left child pointers (right pointers for maximum) until you can't anymore.
• return the last key found

public Node treeMinimum(Node x) {
    while (x.getLeftChild() != null) {
        x = x.getLeftChild();
    }

    return x;
}

public Node treeMaximum(Node x) {
    while (x.getRightChild() != null) {
        x = x.getRightChild();
    }

    return x;
}

Both the procedures run in (O(height)) time.

Successor :
The successor of a node x is the node with smallest key greater than x’s key. To compute the successor of a node x ;

• Easy Case : If x's right subtree is nonempty, return minimum key in right subtree.
• Otherwise : Find the first ancestor y which is also a left child of it's parent z. Then return z.

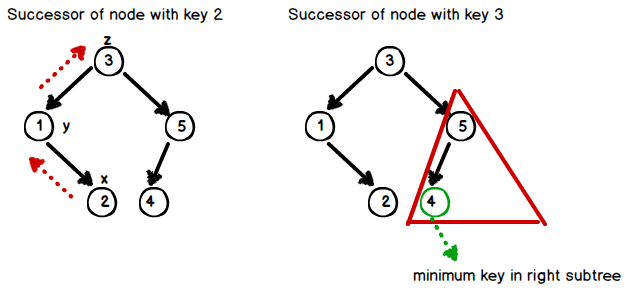
The procedure is as follow;

public Node treeSuccessor(Node x) {
    if (x.getRightChild() != null) {
        return treeMinimum(x.getRightChild());
    }

    Node parent = x.getParent();

    while (parent != null && parent.getRightChild() == x) {
        x = parent;
        parent = x.getParent();
    }

    return parent;
}

Predecessor :
The predecessor of a node x is the node with greatest key less than x’s key. To compute the predecessor of a node x ;

• Easy Case : If x's left subtree is nonempty, return maximum key in left subtree.
• Otherwise : Follow parent pointers until you get to a key less than k.

The procedure is as follow;

public Node treePredecessor(Node x) {
    if (x.getLeftChild() != null) {
        return treeMaximum(x.getLeftChild());
    }

    Node parent = x.getParent();

    while (parent != null && parent.getKey() > x.getKey()) {
        parent = parent.getParent();
    }

    return parent;
}

Both the procedures run in (O(height)) time.

Insertion and Deletion

While insertion and deletion operations the binary search tree property should be preserved.

Insertion :
To insert a key k;

• Search a proper position for x.
• While searching maintain a trailing pointer y which is parent of x.
• Insert x as left / right child of its parent y.

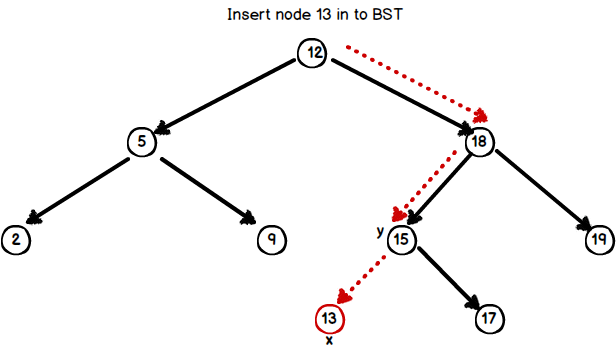
insert procedure is as follows;

public void insert(Node x) {
    Node y = null;
    Node z = root;

    while (z != null) {
        y = z;

        if (x.getKey() <= z.getKey()) {
            z = z.getLeftChild();
        } else {
            z = z.getRightChild();
        }
    }

	// set y as x's parent
    x.setParent(y);

	// if root is already null then set x as root
    if (root == null) {
        root = x;
    } else if (x.getKey() <= y.getKey()) { // set x as left child of its parent y
        y.setLeftChild(x);
    } else { // set x as right child of its parent y
        y.setRightChild(x);
    }
}

The running time of insertion is (O(height)).

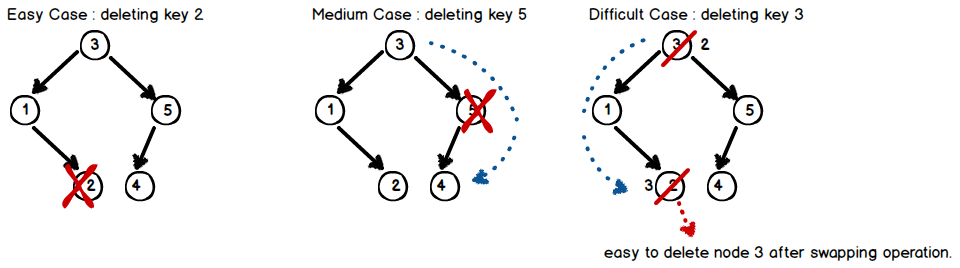
Deletion :
To delete a key k from a search tree;

• Search for k.
• Easy Case (k's no children) : Delete k's node from tree.
• Medium Case (k's one child) : Unique child has to know its parents position.
• Difficult Case (k's two children) : Compute k’s predecessor l, swap them, and deleting l will do the trick.

An illustration of deleting a key for each case;

The delete procedure will use a subroutine which is called transplant to handle with the cases when x has no children, or only one child. Transplant and delete procedures are as follows;

public void delete(int key) {
    Node delNode = search(root, key);

    if (delNode.getLeftChild() == null) {
        transplant(delNode, delNode.getRightChild());
    } else if (delNode.getRightChild() == null) {
        transplant(delNode, delNode.getLeftChild());
    } else {
        Node y = treePredecessor(delNode);
        swapKeys(delNode, y);

        Node z = y.getLeftChild();
        transplant(y, z);
    }
}

private void transplant(Node u, Node v) {
    if (u.getParent() == null) { // we delete the root
        root = v;
     } else if (u.getParent().getLeftChild() == u) {
        u.getParent().setLeftChild(v);
    } else {
        u.getParent().setRightChild(v);
    }

    if (v != null) {
        v.setParent(u.getParent());
    }
}

The running time of delete procedure is (O(height)).

Here you can find the complete implementation of a BST by java.
BST