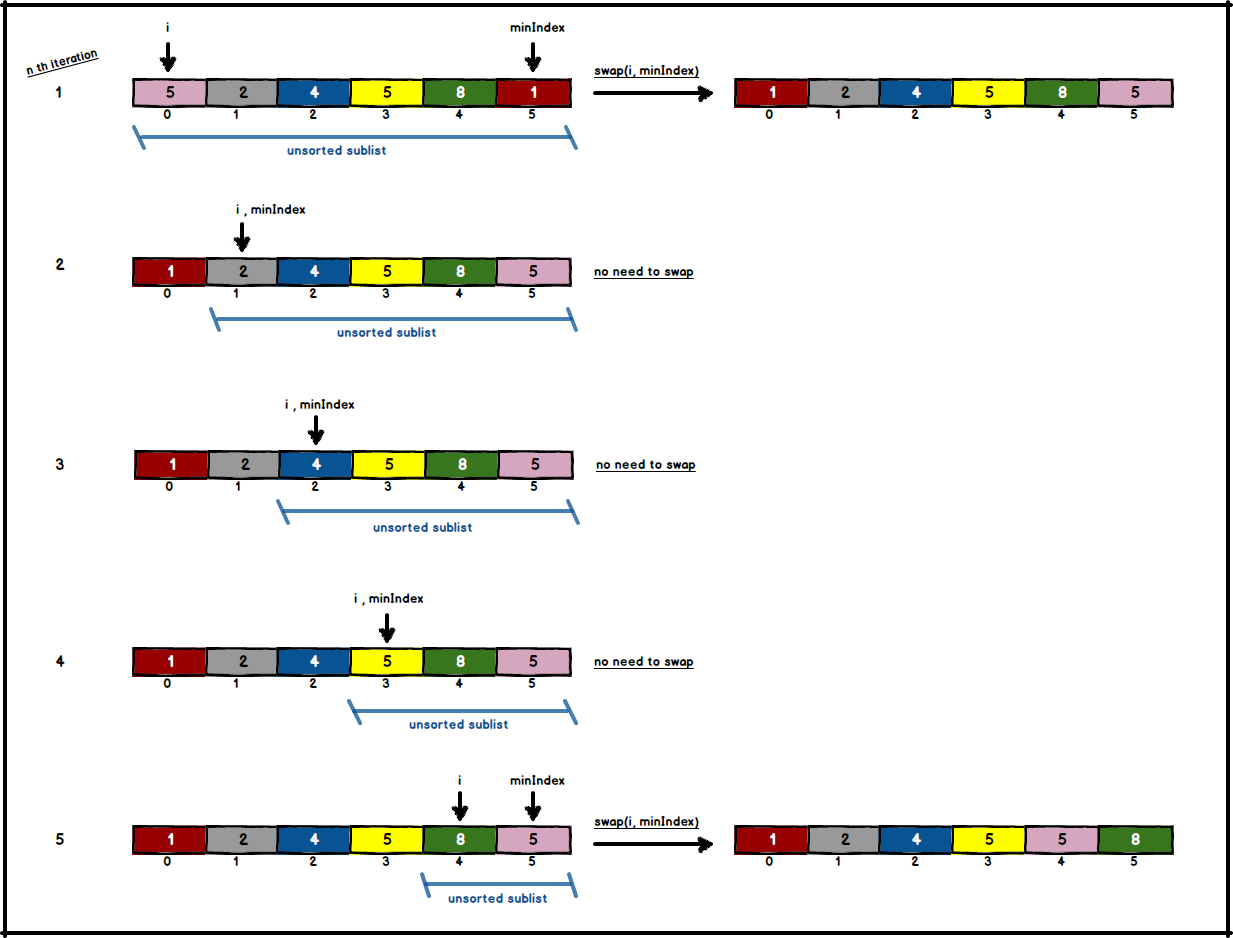
Selection Sort

Selection sort is an in-place comparison sort algorithm which has \( O(n^2) \) running time complexity in both best and worst case. Even though its logic is similar to insertion sort, it’s a very inefficient sorting algorithm. List is both divided into two parts as sorted and unsorted where initially sorted part is empty. Every turn, algorithm finds the minimum (or maximum) key in unsorted sublist then swaps it with the leftmost element of unsorted part. Due to the reason which elements in any place could get swapped selection sort is not stable.

Algorithm

• Find minimum in unsorted list.
• Swap minimum with left most element in unsorted list.
• Shift boundaries of unsorted list to right by one.

Complexity Analysis

Due to the fact that selection sort is not adaptive ( number of cycles doesn’t change due to given order) it takes \( O(n^2) \) for every case.

Time			Space
Best case	Worst case	Average case	Worst case
\(O(n^{2})\)	\(O(n^{2})\)	\(O(n^{2})\)	\(O(1) auxiliary\)

Code

public class SelectionSort {

    public int[] selectionSort(int[] numbers) {
        for (int i = 0; i < numbers.length - 1; i++) {

            int minIndex = i;
            for (int j = i + 1; j < numbers.length; j++) {
                if (numbers[j] < numbers[minIndex]) {
                    minIndex = j;
                }
            }

            if (minIndex != i) {
                swap(i, minIndex, numbers);
            }
        }
        return numbers;
    }

    private void swap(int i, int j, int[] numbers) {
        int temp = numbers[i];
        numbers[i] = numbers[j];
        numbers[j] = temp;
    }
}