Heaps

The binary heap data structure is an array object that represents a nearly complete binary tree. Thus, each element of the array corresponds to a node of the tree. Heaps are useful data structures for heapsort ,and they are underlying data structure of priority queues. So for simplicity we can say priority queue is a synonym for a heap. There are two kind of heaps;

• Max-heaps : Returns the maximum element of the collection.
• Min-heaps : Returns the minimum element of the collection.

This tutorial will continue with min-heaps. Supported operations by a heap is listed below;

Operation	Definition	Time Complexity
Extract-Min	Remove an object in heap with a minimum key value.	\(O(lgn)\)
Insert	Add a new object to a heap	\(O(lgn)\)
Build-Min-Heap	Initialize a heap in linear time for a given set.	\(O(n)\)
Decrease-Key	Decreases the key of an existing node to a given value.	\(O(lgn)\)
Get-Min	Return the min key.	\(O(1)\)

Heap Property

• At every node x; Key[x]   ≤   all keys of x' s children.
• Root has the minimum key.

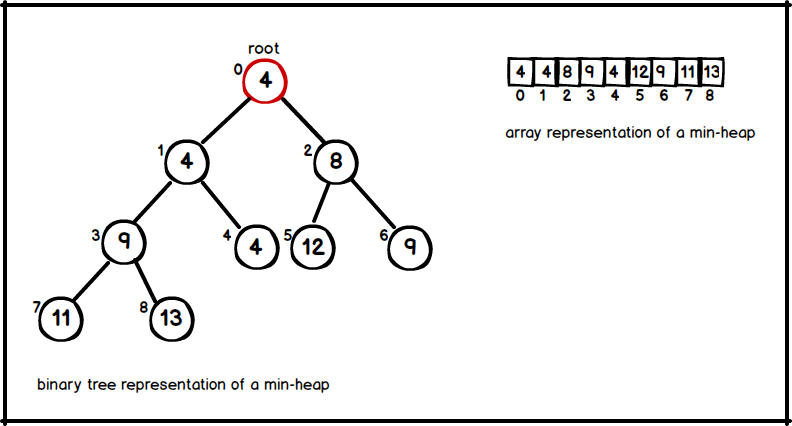
Parent :

parent(i) = \( i/2 \) if i is even / \( ⌊i/2⌋ \) if i is odd

private int parent(int i) {
	return (i - 1) / 2;
}

Left Child :

leftChild(i) = \( 2 * i \)

private int left(int i) {
    return 2 * i + 1;
}

Right Child :

rightChild(i) = \( 2 * i + 1 \)

private int right(int i) {
    return 2 * i + 2;
}

Insert and Bubble-Up

Insertion is a straightforward process for heaps, and takes \( O(lgn) \) time. For a given key k

• Stick k at end of last level.
• Bubble-Up k until heap property is restored.( i.e., key of k' s parent is ≤ k )

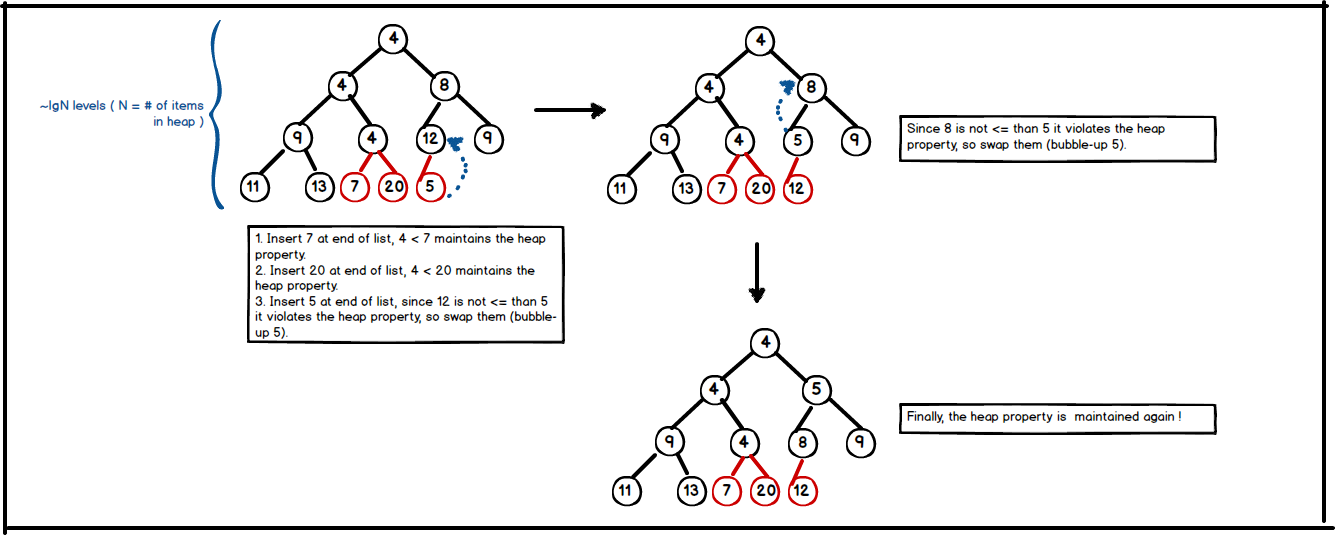
The implementation of insert is as follows;

public void insert(int item) {
	list.add(item);
	int i = list.size() - 1;
	int parent = parent(i);

	while (parent != i && list.get(i) < list.get(parent)) {
		swap(i, parent);
		i = parent;
		parent = parent(i);
	}
}

Extract-Min and Bubble-Down

• Delete last leaf and set it as new root.
• Iteratively Bubble-Down until heap property is maintained. (always swap with smaller child!)

The extractMin procedure uses minHeapify subroutine for bubble-down process, and implementation of both of them can be seen below;

public int extractMin() {

	if (list.size() == 0) {
		throw new IllegalStateException("MinHeap is EMPTY");
	} else if (list.size() == 1) {
		int min = list.remove(0);
		return min;
	}

	// remove the last item ,and set it as new root
	int min = list.get(0);
	int lastItem = list.remove(list.size() - 1);
	list.set(0, lastItem);

	// bubble-down until heap property is maintained
	minHeapify(0);

	// return min key
	return min;
}

private void minHeapify(int i) {
	int left = left(i);
	int right = right(i);
	int smallest = -1;

	// find the smallest key between current node and its children.
	if (left <= list.size() - 1 && list.get(left) < list.get(i)) {
		smallest = left;
	} else {
		smallest = i;
	}

	if (right <= list.size() - 1 && list.get(right) < list.get(smallest)) {
		smallest = right;
	}

	// if the smallest key is not the current key then bubble-down it.
	if (smallest != i) {

		swap(i, smallest);
		minHeapify(smallest);
	}
}

Build-Min-Heap

minHeapify procedure is used when a heap is initialized from an unordered array in linear time. On the other hand, it is proven that iterating only from middle of the array down to its first element is sufficient to build the heap. The buildMinHeap procedure is as follows;

public void buildHeap() {
	for (int i = list.size() / 2; i >= 0; i--) {
		minHeapify(i);
	}
}

Decrease Key

Decreases the key of a node from a given index. So, after decreasing the key of the node the heap property must be maintained, thus node will bubble-up to its correct position. decrease procedure is as follow;

public void decreaseKey(int i, int key) {
	if (list.get(i) < key) {
		throw new IllegalArgumentException("Key is larger than the original key");
	}

	list.set(i,key);
	int parent = parent(i);

	// bubble-up until heap property is maintained
	while (i > 0 && list.get(parent) > list.get(i) ) {

	     swap(i, parent);
	     i = parent;
	     parent = parent(parent);
	}
}

Get-Min

Returns the root from heap in \( O(1) \) time.

public int getMin() {
    return list.get(0);
}

The whole source code of a min-heap can be seen from here.